Source: Perplexity Metric for LLM Evaluation.
About Perplexity
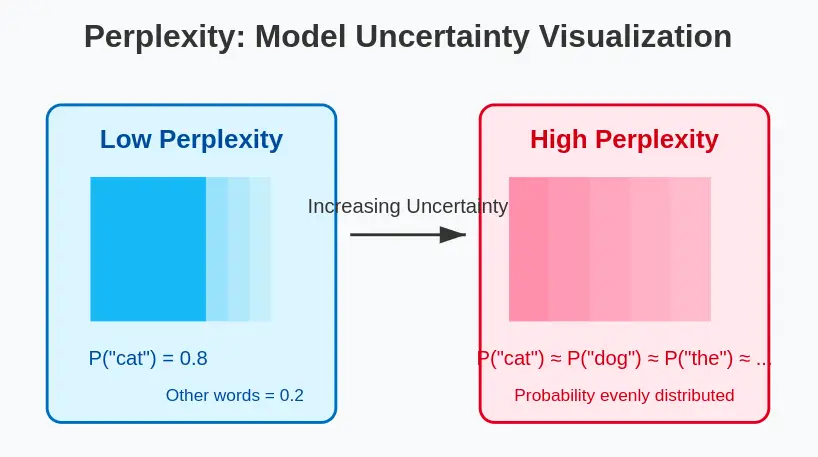
Perplexity is a widely used metric for evaluating language models, measuring how effectively a probability-based model predicts a sequence of words. The term perplexity is used because it intuitively reflects the model’s “uncertainty” in its predictions. Lower perplexity indicates the model is more confident and accurate in generating predictions that closely align with the target text. To better understand perplexity, it might be helpful to capture the concept of probability-based models.
Probability-based model
A Probability-based model is a type of machine learning or statistical model that predicts outcomes based on probabilities. The output is often a distribution over possible outcomes (e.g., a probability for each word in a vocabulary). Here are some examples of the probabilistic models:
- N-gram Models: Predict the next word based on the probabilities of the previous N words.
- Hidden Markov Models (HMMs): Often used in sequential data, such as speech or text processing.
- Language Models: Assign probabilities to sequences of words, such as GPT, BERT (masked language models), and traditional models like RNNs.
Perplexity Definition
Mathematically, for a probability-based model predicting a sequence $w_1, w_2, …, w_N$ , the perplexity is:
Here:
- $P(w_i | w_{1: i-1})$ is the probability of the word $w_i$ given the context (previous words).
- $N$ is the total number of words in the sequence.
How to Understand the Mathematical Formula
To understand the formula of perplexity, we use the language model as an example and interpret it step by step.
Joint Probability of a Sentence
In a language model, $P(w_i | w_{1: i-1})$ represents how likely the model thinks the word $w_i$ is, given all the previous words in the sequence. For a sentence $w_1, w_2, …, w_N$, the model predicts the joint probability of the entire sequence using the product of the conditional probabilities for each word, which is:
Taking the Logarithm
Multiplying probabilities for a long sequence can result in very small numbers, which can lead to numerical underflow for computers
To avoid this, we take the logarithm of the probabilities, transforming probabilities into negative numbers for easy use:
Information Theory
To understand why the formula involves taking the negative logarithm of probabilities, we need to refer to information theory. In information theory, the negative logarithm of a probability corresponds to the information content of an event:
Negative log probability quantifies the model’s “uncertainty” or “surprise” when predicting the correct answer.
For example, a highly likely event (e.g., $P(w_i | w_{1: i-1}) \approx 1 )$ has low information content $( I(w_i) \approx 0 )$, indicating low uncertainty. A rare event (e.g., $P(w_i | w_{1: i-1}) \approx 0.01$ ) has high information content $( I(w_i) \approx 6.64 )$, indicating high uncertainty.
Thus the negative to the logarithm of the probabilities can be interpreted as the uncertainty of the model’s predictions or how surprised the model is by the actual outcome.
Further Transformation
To make the uncertainty of the model’s predictions independent of the length of the sequence $N$, we take the average of the negative log probabilities:
The result of the negative logarithm of probabilities is a value on a logarithmic scale (log-scale), which is not very intuitive for humans. Therefore, by exponentiating the value, we can convert it back into the original probability space, which comes to our final formula:
Interpretation of Perplexity
Now, we can interpret perplexity as the number of choices the model has when predicting the next word. The intuition is that a lower perplexity indicates the model is more confident and accurate in its predictions, with fewer equally likely options for the next word (e.g., a perplexity of 10 suggests 10 plausible choices). In contrast, a higher perplexity reflects greater uncertainty, while a perplexity of 2 suggests the model is highly confident, considering only 2 plausible options.
Use Cases
Quality Assessment: Lower perplexity often correlates with better real-world performance, such as fluency and accuracy in text generation.
Model Evaluation: Perplexity can be used to compare language models during training to select the best-performing model.
Disadvantages
- Although lower perplexity means that the model is more confident of its answer, A low perplexity doesn’t guarantee the generated text is meaningful or coherent.
- Perplexity values depend on the vocabulary size and dataset, so comparing perplexity across different tasks or datasets isn’t always valid.
Perplexity in-action
Here’s a demo that showcases how to calculate perplexity using Python.
import math
def calculate_perplexity(probabilities):
"""
Calculate the perplexity given a list of predicted probabilities.
Formula:
PPL = exp(- (1/N) * sum(log(P(w_i | w_{1:i-1}))))
Args:
probabilities (List[float]): A list of conditional probabilities, where each probability
P(w_i | w_{1:i-1}) represents the model’s predicted likelihood of word w_i
given the preceding context w_{1:i-1}.
Returns:
float: The calculated perplexity.
"""
# Ensure the input is valid
if not probabilities or any(p <= 0 for p in probabilities):
raise ValueError("Probabilities must be a non-empty list with values > 0.")
n = len(probabilities) # This corresponds to N in the formula
log_sum = sum(math.log(p) for p in probabilities) # This corresponds to sum(log(P(w_i | w_{1:i-1}))) in the formula
cross_entropy = -1 / n * log_sum # Cross-entropy = - (1/N) * sum(log(P(w_i | w_{1:i-1})))
perplexity = math.exp(cross_entropy) # PPL = exp(Cross-Entropy)
return perplexity
probabilities = [0.1, 0.2, 0.3, 0.4] # Example word probabilities
perplexity = calculate_perplexity(probabilities)
print(f"Perplexity: {perplexity:.4f}")When to use Perplexity
In addition to foundational model developers using perplexity to evaluate model performance, it can also be applied in other activities. For instance, when building datasets, researchers can use perplexity to measure the difficulty a dataset poses to a model. Legal or medical texts, for example, are often harder to predict than general news articles. For multilingual corpus researchers, perplexity can help compare the diversity and complexity of different languages or corpora, with higher perplexity indicating more complex syntax or a larger vocabulary. Additionally, users of large language models can indirectly adjust perplexity by modifying the temperature or generation strategies to produce more suitable responses.
Video explanation
- Here is a video explaining the evaluation metric of perplexity for language models. In this video, Prof. Dan Jurafsky from Stanford explains Perplexity – intuition, derivation, and limitations:
Related Questions:

