Source: Daily Dose of Data Science
Introduction
Gaussian Mixture Models (GMMs) are a probabilistic approach to clustering that assumes that data is generated from a mixture of multiple Gaussian distributions. Unlike K-means, which assigns each point to a single cluster, GMMs provide a probability distribution over clusters, making them useful for more complex clustering tasks. We will discuss the key pros and cons of GMMs below, especially in comparison with K-Means. The image above depicts a Gaussian Mixture, a function made up of several Gaussian distributions.
Pros of GMMs
Identify local clusters within a dataset:
One of the biggest advantages of GMMs is their ability to identify finer, local clusters within a dataset. When clusters overlap significantly from a global perspective, K-means may fail to differentiate them properly. Because K-means assigns each point to exactly one cluster and assumes clusters are globular and equally sized, they often fail in real-world scenarios where data points lie between multiple cluster centers or where clusters differ in shape, size, or orientation.
GMMs, however, can model these overlapping distributions more effectively by considering the likelihood that a point belongs to multiple clusters. This is particularly effective in domains like speaker identification, where speech features from different speakers may overlap due to accents or recording conditions, or bioinformatics, where gene expression patterns cluster in subtle, continuous ways rather than forming clear-cut groups. GMMs’ probabilistic approach can reflect these ambiguities by assigning soft cluster memberships based on likelihood, capturing complex structures that K-means would oversimplify.
Soft Clustering:
Unlike K-means, which assigns each point to a single cluster (hard clustering), GMMs provides probability estimates, an approach known as soft clustering. This means that each data point has a probability of belonging to multiple clusters. This probabilistic approach is particularly useful in cases where data points exist at the boundaries between clusters, such as in topic modeling or customer segmentation.
Clusters of flexible shape and size:
GMMs offer increased flexibility by allowing users to specify different covariance structures for clusters. This means clusters can take on various shapes: elliptical, spherical, or otherwise rather than being limited to the compact, circular clusters that K-means typically forms. This adaptability makes GMMs well-suited for datasets where clusters have varying densities or orientations.
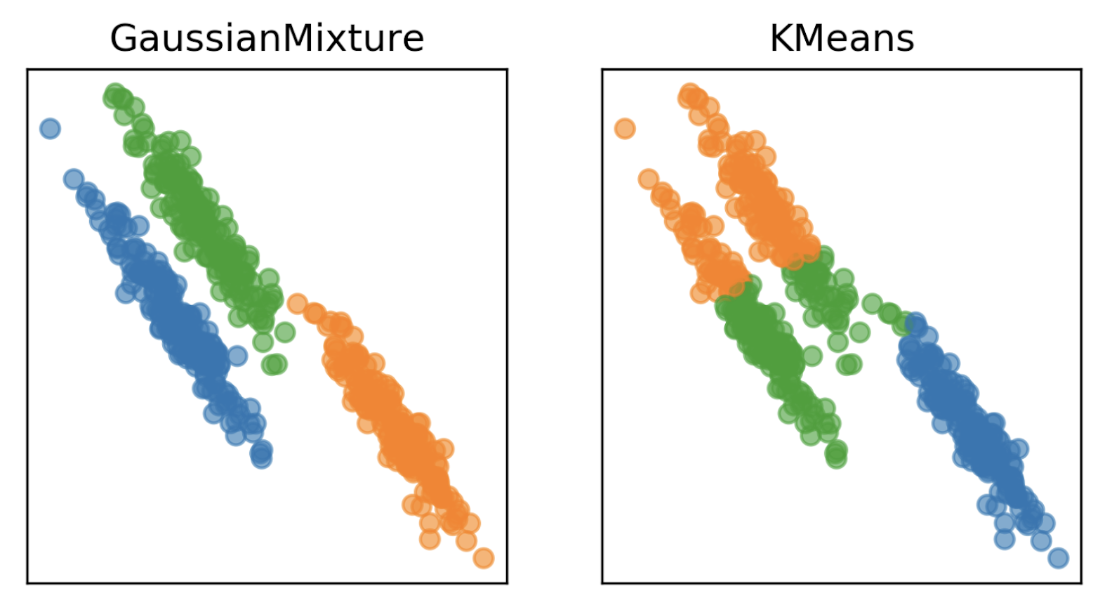
Source: Applied Machine Learning in Python
In the above example, we can see that while K-Means is restricted by its compact, circular clusters, GMMs are able to support more flexible shapes.
Cons of GMMs
Problem of local convergence:
A significant drawback of GMMs is that, like K-means, they rely on an iterative optimization process that may converge to a local minimum rather than the best possible solution. This means running the algorithm multiple times on the same dataset with the same number of components could yield different clustering results. This sensitivity to initialization can be mitigated by using techniques such as Expectation-Maximization (EM) with careful initialization strategies.
Computationally intensive:
Another drawback of GMMs is that they are more computationally intensive than K-means. This is because they estimate not only cluster means but also covariances and mixing coefficients during each EM iteration. This complexity increases processing time and memory usage, especially for high-dimensional datasets or when modeling clusters with full covariance matrices.
Uses large number of parameters:
Another challenge with GMMs is their reliance on estimating a large number of parameters. This includes the means, covariances, and mixture weights for each component. If the dataset is small or contains noise, this flexibility can lead to overfitting.
Not very scalable:
Because GMMs involve repeated computation of probabilities and matrix operations, they can struggle with scalability. Large datasets or high-dimensional data may significantly slow down convergence and make the algorithm impractical.
Conclusion
GMMs provide a powerful alternative to K-means by allowing for soft clustering, handling overlapping clusters, and offering cluster shape flexibility. However, their tendency to converge to local optima can make results inconsistent across runs. Understanding these strengths and weaknesses of GMMs can help practitioners determine when GMMs are the best choice for a given clustering task.
TL;DR: Pros and Cons of GMMs in short format
Pros of GMM
- Has the ability to find more local clusters that K-Means would not be able to differentiate when there is a lot of overlap from a global view
- Provides probability estimates of belonging to each cluster (soft clustering)
- Increased flexibility provided by having ability to specify covariance structure
Cons of GMM
- Not guaranteed to converge to global optimum. If algorithm is run multiple times on the same data set with the same number of components, the cluster assignments might be different
- GMMs are more computationally intensive than K-means
- Requires estimating many parameters (means, covariances, and weights), which can lead to overfitting in small datasets
- Can struggle with very large datasets due to EM iterations
Videos for Further Learning
- Gaussian Mixture Models (GMM) Explained provides a great overview of how GMMs work (runtime: 5 minutes)
- CAIS Presents Clustering (Kmeans Vs. Gaussian Mixture Models) Lecture provides a comprehensive comparison of K-Means and GMMs (runtime: 42 minutes)
Related Articles


