Source: Perpetual Enigma
Introduction
K-means clustering is one of the most popular unsupervised machine learning algorithms used for partitioning data into distinct groups based on similarity. It works by iteratively assigning data points to the nearest centroid and updating centroids until convergence. Despite its widespread use in data science, K-means clustering has both advantages and limitations. Below, we explore the key pros and cons of K-means clustering algorithm.
Pros of K-Means
- Easy to implement: One of the biggest advantages of K-means clustering is its simplicity. The algorithm is straightforward to implement using common programming languages like Python and R, with libraries such as scikit-learn providing built-in functions for quick application. Due to its efficiency, K-means is widely used in various domains, including customer segmentation, image compression, and anomaly detection.
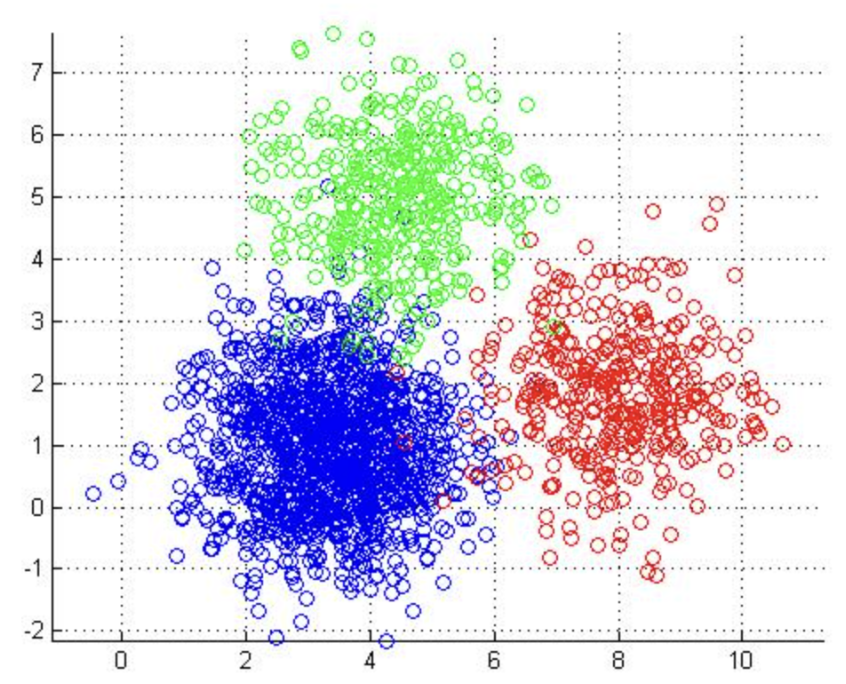
- Produces compact, spherical clusters: K-means works well when the underlying data clusters are spherical or globular in shape. Since it minimizes variance within clusters, the resulting groups tend to be tightly packed and well-separated, which is useful in applications where distinct, compact clusters are expected. This property makes K-means particularly effective in cases like document classification and marketing segmentation, where well-defined clusters are often desirable.
Cons of K-Means
- Must specify number of clusters in advance: A major drawback of K-means is the requirement to define the number of clusters (K) beforehand. If the correct value of K is unknown, users must experiment with different values or use techniques like the Elbow Method or Silhouette Analysis to estimate an optimal number. This limitation can make the algorithm less flexible, especially when working with complex datasets where the number of natural groupings is unclear.
- Sensitive to initial choices of centroids: The algorithm’s outcome heavily depends on the initial placement of centroids. Poor initialization can lead to suboptimal clustering or convergence to a local minimum rather than the global best solution. To mitigate this, strategies such as K-means++ initialization help improve centroid selection, reducing the chances of poor clustering results.
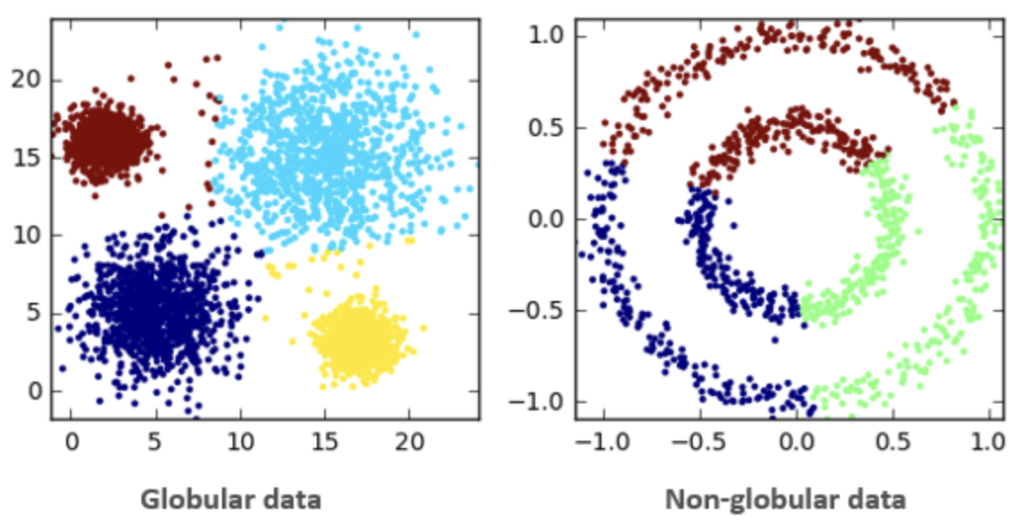
- Not good at identifying clusters that don’t follow a globular shape
Source: Shiksha Online
K-means assumes that clusters are roughly spherical, making it ineffective for datasets containing irregularly shaped or overlapping clusters. For instance, in cases where clusters are elongated, have varying densities, or contain outliers, K-means may misclassify points. As shown in the example above, K-means struggles with classifying data in non-globular shapes. Alternative clustering methods like DBSCAN or hierarchical clustering are better suited for such scenarios.
Conclusion
K-means clustering is a powerful and efficient algorithm for partitioning data, particularly when working with well-separated, compact clusters. However, its reliance on predefined cluster numbers, sensitivity to initialization, and difficulty handling non-globular shapes highlight some of its limitations. Understanding these pros and cons helps practitioners decide when K-means is appropriate and when alternative clustering methods should be considered.
TL;DR: Here is the complete list in short format:
Pros of K-Means Clustering
- Easy to implement
- Produces compact, spherical clusters
Cons of K-Means Clustering
- Must specify number of clusters in advance
- Sensitive to initial choices of centroids
- Not good at identifying clusters that don’t follow a globular shape
Videos for Further Learning
- To get a good grasp on what K-means clustering is, watch StatQuest: K-means clustering (runtime: 9 minutes)
- To understand how to apply the Elbow Method and Silhouette Coefficient method for K-means, watch Elbow Method | Silhouette Coefficient Method in K Means Clustering Solved Example by Mahesh Huddar (runtime: 10 minutes)
- To learn how to choose good initial centroids, watch Choosing Initial Centroids in K-Means Algorithm (runtime: 15 minutes)
Related Articles



