
Source: Mao Mao’s Blog
Introduction
Dimensionality reduction is a foundational concept in data science and machine learning, addressing one of the most significant challenges when dealing with datasets: the “Curse of Dimensionality.” As the number of features in a dataset grows, several things happen. Computational complexity increases, models become more prone to overfitting, and data sparsity can degrade performance. Dimensionality reduction techniques mitigate these issues by representing a dataset using fewer features (dimensions) while preserving its meaningful properties. This enables more efficient processing and improving the generalizability of machine learning models.
The Curse of Dimensionality
In order to understand the problems caused by higher dimensions, we first need to understand the Curse of Dimensionality. It refers to issues that occur in high-dimensional datasets that do not exist in low-dimensional datasets. As the number of dimensions increases, several issues emerge that can hinder data analysis and machine learning performance. One major problem is computational inefficiency. The resources required to process, store, and analyze data grow exponentially with the number of dimensions, making many algorithms impractical for large datasets. Additionally, overfitting becomes a concern, as models trained on high-dimensional data often capture noise rather than meaningful patterns, leading to poor generalization on new data.
Another issue is data sparsity, where data points become increasingly spread out in high-dimensional spaces. This reduces the density of samples within any given region. This sparsity makes it difficult for models to identify reliable patterns and can degrade the performance of distance-based methods such as k-nearest neighbors (k-NN) and clustering algorithms. A consequence of this is the “No Nearby Neighbors” phenomenon, which affects all distance- and similarity-based machine learning methods. As the number of dimensions increase, even the closest data points become far apart, and this in turn reduces the effectiveness of algorithms that rely on proximity measures.
These challenges make it difficult to extract valuable insights, build effective models, and achieve generalization in high-dimensional spaces. As a result, methods to reduce dimensionality while preserving essential information are increasingly necessary.

Source: IBM
Dimensionality Reduction
Dimensionality reduction techniques aim to solve this problem by reducing the number of input variables or features in a dataset while preserving its essential structure and information. This process is not only crucial for improving computational efficiency but also for uncovering hidden patterns in data that might otherwise remain obscured in higher dimensions.

Source: Roboflow
Fields Where High-Dimensional Data is Common
High-dimensional datasets are prevalent in a variety of fields:
- In Computer Vision, images often consist of thousands or even millions of pixels, each representing a dimension. Without dimensionality reduction, analyzing and modeling such data would be computationally prohibitive.
- In Genomics, genetic data contains thousands of variables, such as genes or single nucleotide polymorphisms (SNPs). Dimensionality reduction helps identify the most relevant features for understanding diseases or biological processes.
- In Natural Language Processing (NLP), text data is often represented in high-dimensional vector spaces, such as TF-IDF or word embeddings. Here, dimensionality reduction techniques can uncover underlying topics or themes.
Dimensionality Reduction in Information Retrieval (IR)
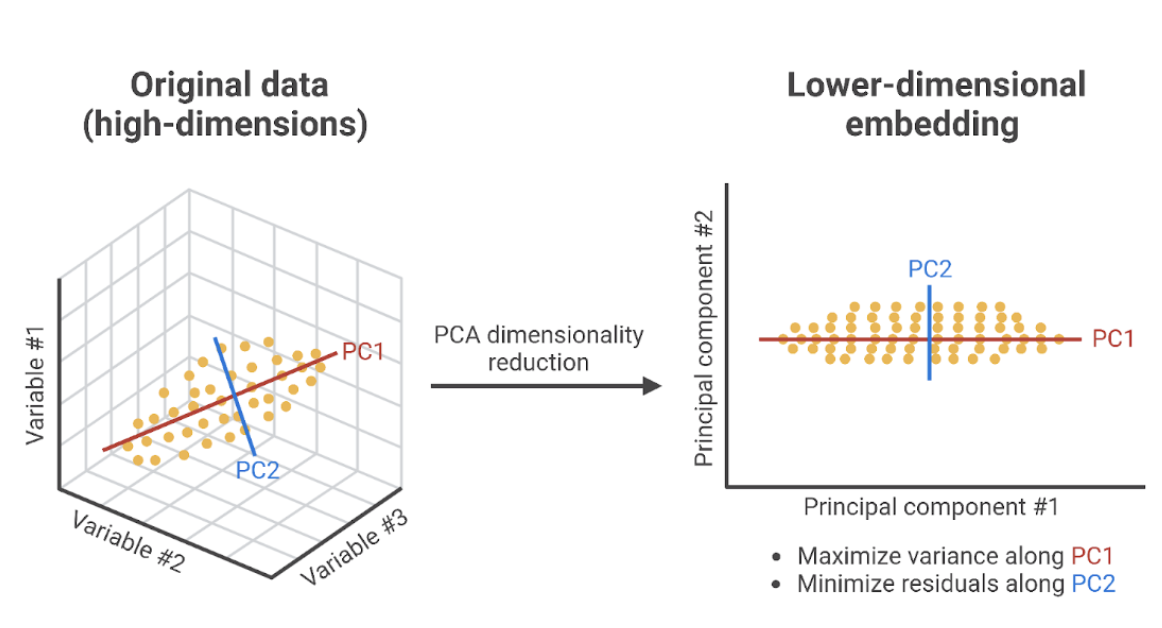
Information Retrieval (IR) is one field where dimensionality reduction plays a critical role. Search engines, for example, often need to process large corpora of text data, represented in high-dimensional vector spaces. We can use techniques like Principal Component Analysis (PCA) to reduce the dimensionality of text data by identifying latent structures or topics, making the data easier to work with and improving retrieval accuracy.
Principal Component Analysis (PCA) transforms high-dimensional data into a smaller number of components by identifying the directions (principal components) that capture the most variance. This is particularly useful for text embeddings, as it retains the most important patterns while reducing dimensional complexity.
Source: 123 of AI
Feature Extraction vs. Feature Selection
Dimensionality reduction can be broadly categorized into two approaches: feature extraction and feature selection.
Feature Extraction
Feature Extraction creates new features by transforming the original raw dataset into a more meaningful format. This includes combining and/or reducing multiple features into a smaller number of new features. For example, Principal Component Analysis (PCA) generates new features called “principal components” that summarize the variance in the data.
Feature Selection
Feature Selection involves selecting a subset of the most relevant features from the original dataset. For instance, in a dataset with 1,000 features, feature selection might retain only 50 features that are most informative, discarding the rest. This helps improve the model and combats the curse of dimensionality. Features are selected as they are, so unlike feature extraction, no new features are being created.
The image below illustrates the differences between Features Selection and Feature Extraction. Feature Extraction creates new features (denoted by the circles with new colors) by combining the original input features, while Feature Selection merely chooses several of the original input features (denoted by squares with the same colors).

Source: Viso.ai
Both Feature Extraction and Feature Selection aim to simplify the dataset while preserving its meaningful properties.
Methods of Dimensionality Reduction: Feature Extraction Techniques
Feature Extraction Dimensionality Reduction methods are typically divided into two categories: linear and non-linear techniques.
Linear Methods
Linear Methods assume that the data lies on a low-dimensional linear subspace. These methods are computationally efficient and widely used for their simplicity.
- Principal Component Analysis (PCA): PCA is one of the most popular linear methods. It identifies the directions (principal components) along which the variance in the data is maximized. By projecting the data onto these components, PCA reduces the number of dimensions while retaining the most significant information.
- Non-Negative Matrix Factorization (NMF): NMF decomposes a data matrix into two smaller non-negative matrices. This makes it particularly useful for applications where negative values do not make sense, such as in image processing or text analysis.
- Linear Discriminant Analysis (LDA): LDA is another linear dimensionality reduction technique, but unlike PCA, which focuses on maximizing variance, LDA aims to maximize the separation between predefined classes. It does this by finding a linear combination of features that best separates different categories in the data, making it particularly useful for supervised classification tasks. LDA is common in fields like pattern recognition and face recognition, where distinguishing between classes is critical.
Non-Linear Methods
Non-linear methods are designed to handle datasets that cannot be adequately represented using linear techniques. These methods capture complex, non-linear relationships between variables.
- Autoencoder: Unlike linear techniques like PCA and SVD, autoencoders are neural network-based models that perform nonlinear dimensionality reduction. They consist of an encoder that compresses input data into a lower-dimensional representation and a decoder that reconstructs the original data from this compressed form. By learning complex, nonlinear transformations, autoencoders can capture intricate patterns in high-dimensional data. This makes them especially useful for text embeddings, anomaly detection, and feature extraction in Information Retrieval.
- t-SNE (t-Distributed Stochastic Neighbor Embedding): t-SNE is widely used for visualizing high-dimensional data in two or three dimensions. It works by preserving the local structure of the data, making it an excellent choice for exploring clusters in datasets like image or text embeddings. However, it performs poorly at preserving distances and densities, so it is not recommended for tasks like clustering or outlier detection.
Methods of Dimensionality Reduction: Feature Selection Techniques
Feature Selection Dimensionality Reduction methods aim to reduce dimensionality by selecting a subset of the most relevant features from the original dataset, rather than transforming the features into a new space. These methods help improve model interpretability, reduce overfitting, and enhance computational efficiency.
- LASSO (Least Absolute Shrinkage and Selection Operator): LASSO is a regression-based technique that applies L1 regularization, which shrinks less important feature coefficients to zero, and ultimately selecting only the most relevant variables. It is common for feature selection in high-dimensional datasets.
- Forward-Backward Selection: This iterative approach selects features by adding (forward selection) or removing (backward elimination) them based on their impact on model performance. It balances complexity and accuracy, making it a practical method for reducing dimensionality in predictive modeling.
- Random Forest Feature Importance: Random forests provide a built-in feature selection mechanism by measuring how much each feature contributes to reducing impurity in decision trees. Features with low importance scores can be removed, streamlining models without significantly impacting performance.
- SHAP (SHapley Additive exPlanations): SHAP values quantify the contribution of each feature to a model’s predictions. By analyzing these values, less influential features can be discarded, helping to reduce dimensionality while maintaining interpretability in complex models.
Applications and Benefits
Dimensionality reduction has a wide range of applications across industries:
- Data Visualization: Reducing data to two or three dimensions allows researchers to visualize complex patterns, identify clusters, and gain intuitive insights.
- Model Efficiency: Machine learning models trained on lower-dimensional datasets are faster to train and less prone to overfitting, leading to better generalization performance.
- Noise Reduction: By discarding less relevant dimensions, dimensionality reduction can help remove noise and improve the quality of analysis.
- Compression: Dimensionality reduction techniques like PCA are often used for data compression, enabling efficient storage and transmission.
Challenges in Dimensionality Reduction
While dimensionality reduction offers many benefits, it also comes with challenges. Reducing dimensions inevitably involves discarding some information, and this information loss can affect the accuracy of downstream tasks. In addition, selecting the right dimensionality reduction technique depends on the specific dataset and application, as improper choices can lead to inferior results. Another thing to note is that identifying the optimal number of dimensions is challenging and requires balancing information retention with simplification. Reducing too much can lead to loss of critical data, while reducing too little may not provide meaningful benefits.
Videos for Further Learning
- StatQuest: PCA main ideas in only 5 minutes!!! by Josh Starmer provides a synthesis of the main ideas from PCA (Runtime: 6 minutes)
- Dimensionality Reduction from Udacity provides a simple, intuitive introduction to Dimensionality Reduction (Runtime: 3 minutes)
Dimensionality Reduction by Udacity
Related Articles


