Both a probability mass function (PMF), in the discrete random variable case, and probability density function (PDF), in the continuous random variable case, show the likelihood of each event in the sample space occurring out of the set of all possible outcomes. The PMF and PDF are non-negative functions that sum or integrate, respectively, to 1. A Cumulative Distribution Function (CDF) is a non-decreasing function such that for a given value x of random variable X, F(X) = P(X <= x). As the CDF is a valid probability, its values range from 0 to 1. As the values of the random variable increase across its support, the CDF accumulates the probability of any event up to that point being observed, and when it reaches 1, it has accounted for all events in the sample space.
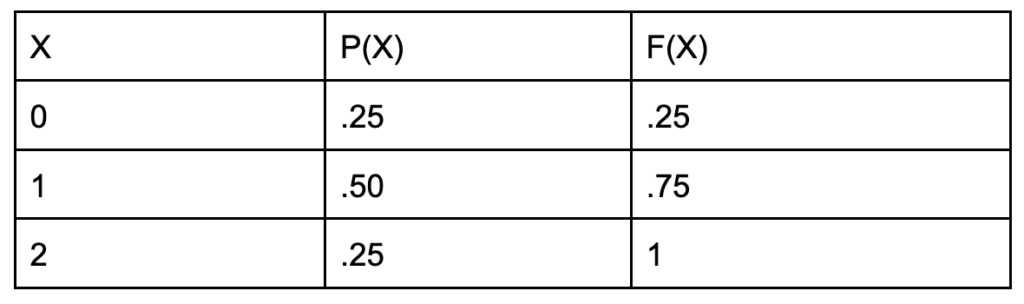
As a simple example, consider X as a random variable that denotes the number of heads observed from flipping a fair coin two times. The support, or range of values X can take on, is {0 1, 2}. The probability of observing 0, 1, and 2 heads, respectively, is .25, .50, and .75, which corresponds to the PMF. The probability of observing <= 0 heads is .25, <=1 heads is .75, and <=2 heads is 1, which provides the values for the CDF.